小学生也能听懂的多项式乘法
什么是多项式
形如
$$y = \sum_{i = 0} ^ {n - 1}a_i \times x ^ i$$
的代数式叫做关于$x$的多项式
为了便于理解,我们有时把它展开来写
$$ y = a _ 0 + a _ 1 x + a _ 2 x ^ 2 + a _ 3 x ^ 3 + ... + a _ {n - 1} x ^ {n - 1}$$
多项式的运算
加法
等次数项系数相加,最后再相加。初中数学大家都学过。
减法
有人说过:减法也是加法。
乘法
把一个多项式的每一项分别于另一个多项式的所有项相乘,最后再相加。
我们可以写成这样:
设
$$f(x) = \sum _ {i = 0} ^ {n - 1} a _ i x ^ i$$
$$g(x) = \sum _ {i = 0} ^ {n - 1} b _ i x ^ i$$
则
$$f(x) * g(x) = \sum _ {i = 0} ^ {n - 1} \sum _ {j = 0} ^ {n - 1} (a _ i + b _ j) x ^ {i + j}$$
很好理解是不是
优化
显然,多项式乘法我们需要两层for循环,所以是$O(n ^ 2)$的复杂度。
能不能用一些奇怪操作让两个多项式$O(n)$相乘?
我们想一些初中的知识:
我们想知道一次函数的解析式,我们只要知道函数上两个不同的点的坐标,就可以解出来。
我们想知道二次函数的解析式,我们只要知道函数上三个不同的点的坐标,就可以解出来。
显然,我们想知道$n - 1$次函数的解析式,我们知道函数上$n$个不同的点的坐标,就可以解出来。
由于这个函数被这$n$个点唯一确定,我们可以直接用这$n$个点表示这个函数。所以,我们将这种方式称作函数的点值表示。
显然,我们设$f(x)$过$(x, y _ 1)$,$g(x)$过$(x, y _ 2)$
那么如果$h(x) = f(x) * g(x)$,显然$h(x)$过$(x, y _ 1 \times y _ 2)$
那么我们知道两个函数的点值表示,且这些点值的$x$一样,那么只要把$y$值挨个乘起来,就能得到两个函数乘积的点值表示,复杂度显然是$O(n)$。
假设我们随机找$n$个点,使用秦九韶定理求出点值表示需要$O(n ^ 2)$,想要复原成系数,又需要$O(n ^ 3)$来待定系数解方程。所以我们需要借助一些特定的点来优化。
接下来的内容是学习如何找到这些特定的点。
复数与单位根
复数
复数就是实数与虚数的和,也就是$a+bi$ ,其中$i=\sqrt{(-1)}$ 。如果我们想要数形结合表示一个复数,那么我们可以像用数轴表示实数那样,用平面直角坐标系上的一个点表示一个复数,其中实数和虚数分别用两个维度来表示。
复数的加法和减法很简单,就是实数和虚数部分分别相加减。
根据$i$的定义,我们也不难想出怎么将两个复数相乘,$(a + bi )( c + di) = (ac - bd) + (ad + bc)i$
那么我们自然可以封装一个复数struct,代码不给了,最后一起给。
单位根
在复平面上,以原点为圆心,$1$为半径作圆,所得的圆叫单位圆。可以发现,单位圆上的两个复数相乘,结果仍在单位圆上,且幅角等于原来两个复数的幅角之和。
所以,以原点为起点,圆的 $n$ 等分点为终点,做 $n$ 个向量,设幅角为正且最小的向量对应的复数为$\omega_n$,称为$n$次单位根。显然,其余$n - 1$个复数为$\omega_n^2, \omega_n^3, ..., \omega_n^n$。$\omega_n^n$和$\omega_n^0$在轴上,为$1$。
通俗一点说,把圆周分为$n$份,从$x$轴正半轴逆时针出发,第一份的位置用复数表示就是$n$的单位根,它的$x$次方就是第$x$份
它的性质如下:
- $\omega_{2n}^{2k} = \omega_n^k$。感性理解一下,分成$n$份转$k$格和分成$2n$份转$2k$格显然是一个位置。
- $\omega_n^{k+\frac{n}{2}} = -\omega_n^k$。感性理解一下,转一个半圆和与原点作对称是等效的。
离散傅里叶变换(DFT)
讲了一些前置知识,就是为了铺垫我们的正题——快速傅里叶变换,也就是快速将多项式点值表示与系数表示互换的办法。
我们可以将$f(x)$的$x$选择为$n$的$n$个单位根,当然不是暴力挨个代进去,而是进行分治处理。
我们把
$$f(x) = a_0 + a_1x + a_2x^2 + ... + a_{n - 1}x^{n - 1}$$
按照奇偶分组
$$f(x) = (a_0 + a_2x^2 + ... + a_{n - 2}x^{n - 2}) + ({a_1x + a_3x^3 + ... + a_{n - 1}x^{n - 1}})$$
设
$$f_0(x) = a_0 + a_2x + ... + a_{n - 2}x^{\frac{n - 2}{2}}$$
$$f_1(x) = a_1 + a_3x + ... + a_{n - 1}x^{\frac{n - 2}{2}}$$
显然
$$f(x) = f_0(x ^ 2) + xf_1(x ^ 2)$$
我们将刚刚单位根的两条性质代进去,整理得
$$f(\omega_n^k) = f_0(\omega_n^{2k}) + \omega_n^kf_1(\omega_n^{2k})$$
$$f(\omega_n^{k + \frac{n}{2}}) = f_0(\omega_n^{2k}) - \omega_n^{k}f_1(\omega_n^{2k})$$
两者实部相同,只有虚部相反。因此在算第一个时可以同时算出第二个。问题就这样缩小了一半。而由于缩小后的问题仍能这样解决,我们就可以递归下去,复杂度便优化到了$nlogn$级别。需要注意的是,为了方便编码,我们把次数补成$2^k - 1$次。
考虑把它改为非递归。
观察奇偶分组前和最后分组完的结果。
0 1 2 3 4 5 6 7
0 4 2 6 1 5 3 7
转化为二进制
000 001 010 011 100 101 110 111
000 100 010 110 001 101 011 111
我们会发现,就是把所有的二进制左右颠倒就OK了。这样,我们可以用一些奇奇怪怪的位运算来处理这个反转二进制位数的过程,这就是著名的蝴蝶变换
for (int i = 0; i < limit; i++) {
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
}原理感性理解吧
离散傅里叶逆变换(IDFT)
考虑把处理完的点值表示转化回系数。我们同样可以利用单位根的性质把复杂度优化成$nlogn$。
直接给结论,证明我也证不明白,应该跟前面差不多。
$$a_k = \frac{\sum ^ {n - 1} _ {i = 0} f(\omega ^ i _ n) \times (\omega _ n ^ {-k}) ^ i}{n}$$
总结一下
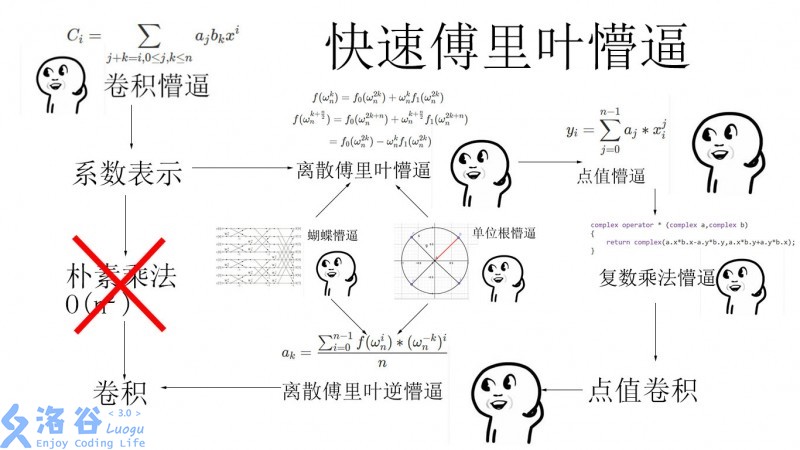
DFT的应用
摘自SuperJvRuo学长的博客
MP3作为一种有损压缩格式,通过剔除掉音乐中特定人耳听觉不敏感的频段,减少数据量,获得更大的压缩比。这个“剔除”的过程就用了DFT。
基于Vocaloid歌声合成软件的初音未来,其合成过程用到了大量的DFT。Vocaloid的合成原理基于STFT(短时傅立叶变换),单音轨合成,每秒至少要进行344次2048点FFT,从而修改信号的频谱特征,Vocaloid合成时大部分时间花在FFT上。所以,你的老婆就是DFT!
汤姆猫之类的变声器使用DFT改变声音的频谱特征。
均衡器,它通过DFT增强或削弱声音中某个特定频率范围的强度。提高高频和低频部分可以让音乐更明亮有节奏感。
降噪器通过DFT减弱声音中含有噪音的频段,从而实现降噪。我们的手机、电脑的声卡也一般具有降噪器,让你的麦克风输出质量更高。
DFT不仅可以用于音频处理,还可以用于图像处理:给图片加一个水印,直接贴在图片上,很容易被抹掉。一种合理的方法是DFT,在频谱上添加高频水印,再IDFT。
代码实现
多项式乘法
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const double PI = std :: acos(-1);
const int MAXN = 1e7 + 5;
struct Complex{
double x, y;
Complex() {}
Complex(double a, double b) {
x = a;
y = b;
}
}a[MAXN], b[MAXN], c[MAXN];
int n, m;
int l, r[MAXN];
int limit = 1;
Complex operator + (const Complex &a, const Complex &b) {
return Complex(a.x + b.x, a.y + b.y);
}
Complex operator - (const Complex &a, const Complex &b) {
return Complex(a.x - b.x, a.y - b.y);
}
Complex operator * (const Complex &a, const Complex &b) {
return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);
}
void FFT(Complex *A, int opt) {
for (int i = 0; i < limit; i++) {
if (i < r[i]) swap(A[i], A[r[i]]);
}
for (int mid = 1; mid < limit; mid <<= 1) {
Complex Wn(cos(PI / mid), opt * sin(PI / mid));
for (int R = mid << 1, j = 0; j < limit; j += R) {
Complex omega(1, 0);
for (int k = 0; k < mid; k++, omega = omega * Wn) {
Complex x = A[j + k], y = omega * A[j + mid + k];
A[j + k] = x + y;
A[j + mid + k] = x - y;
}
}
}
}
int main() {
ios :: sync_with_stdio(false); cin.tie(NULL);
cin >> n >> m;
for (int i = 0; i <= n; i++) cin >> a[i].x;
for (int i = 0; i <= m; i++) cin >> b[i].x;
while (limit <= n + m) {
limit <<= 1;
l++;
}
for (int i = 0; i < limit; i++) {
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
}
FFT(a, 1);
FFT(b, 1);
for (int i = 0; i <= limit; i++) c[i] = a[i] * b[i];
FFT(c, -1);
for (int i= 0; i <= n + m; i++) cout << (int)(c[i].x / limit + 0.5) << " ";
return 0;
}版权属于:Noire02
本文链接:https://noire02.moe/archives/211.html
北京第三区交通委提醒您:复制千万条,版权第一条。转载删出处,博主两行泪。




0 条评论